3.4.3 Conjugate
| Subject | Transformation |
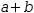 | 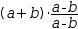 |
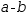 | 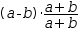 |
 | 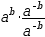 |
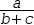 | 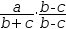 |
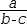 |  |
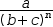 | 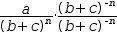 |
Conjugations are useful when attempting to invert an expression. For example,
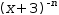
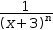

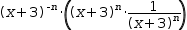
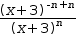
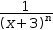
See also Invert .
| Subject | Transformation |
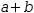 | 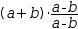 |
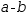 | 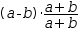 |
 | 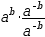 |
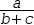 | 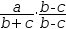 |
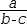 |  |
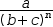 | 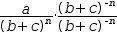 |
Conjugations are useful when attempting to invert an expression. For example,
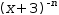
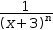

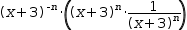
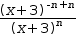
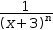
See also Invert .